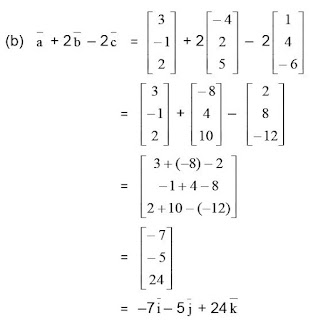(1) Pengertian
Vektor satuan adalah sebuah vektor yang panjangnya satu satuan.
Vektor basis adalah vektor satuan yang arahnya searah dengan sumbu-sumbu koordinat.
Terdapat tiga macam vektor basis, yaitu:
i yaitu vetor basis yang searah dengan arah sumbu X positip
j yaitu vetor basis yang searah dengan arah sumbu Y positip
k yaitu vetor basis yang searah dengan arah sumbu Z positip
Menyatakan vektor a secara analitis yaitu menyatakannya
dalam bentuk persamaan dengan komponen i , j dan k dan dinyatakan sebagai
02. Pada gambar balok dibawah,

nyatakanlah vektor-vektor berikut ini dalam bentuk persamaan vektor
(a) EG
(b) DC
(c) CE
(d) DB


03. Diketahui balok OABC.DEFG dimana O adalah pusat koordinat Cartesius. Jika panjang sisi OA = 4 cm, OC = 7 cm dan OD = 5 cm. Tentukanlah
04. Diketahui titik A(2, –4, 1) dan B(5, –3, –2). Tentukanlah persamaan vector AB
Jawab
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
05. Jika a = 3 i – j + 2 k , b = –4i + 2 j + 5 k dan c = i + 4 j – 6 k , tentukanlah hasil dari :
(a) 2 a – b + 3 c
(b) a + 2 b – 2 c
Jawab
06. Diketahui titik A(4, –3, –2) dan B(2, 1, –3). Jika AB + BC = –9 + 4 + 6 , maka tentukanlah koordinat titik C
Jawab
Misalkan koordinat C(x, y, z), maka
Jadi
x – 2 = –7 maka x = –5
y – 2 = 0 maka y = 2
z + 3 = 7 maka z = 4
Vektor satuan adalah sebuah vektor yang panjangnya satu satuan.
Vektor basis adalah vektor satuan yang arahnya searah dengan sumbu-sumbu koordinat.
Terdapat tiga macam vektor basis, yaitu:
i yaitu vetor basis yang searah dengan arah sumbu X positip
j yaitu vetor basis yang searah dengan arah sumbu Y positip
k yaitu vetor basis yang searah dengan arah sumbu Z positip
Menyatakan vektor a secara analitis yaitu menyatakannya
dalam bentuk persamaan dengan komponen i , j dan k dan dinyatakan sebagai
Jika vektor a = a1 i + a2 j + a3 k
maka panjang vektor a dapat dirumuskan
Vektor, juga dapat terbentuk dari dua titik, misalkan titik A dan titik B merupakan titik pada dimensi tiga, sehingga berlaku
Sebagai pelengkap pemahaman materi, berikut ini diberikan beberapa contoh soal sebagai berikut:
01. Gambarlah vector = 3i + 5j + 4k
Jawab
02. Pada gambar balok dibawah,

nyatakanlah vektor-vektor berikut ini dalam bentuk persamaan vektor
(a) EG
(b) DC
(c) CE
(d) DB


03. Diketahui balok OABC.DEFG dimana O adalah pusat koordinat Cartesius. Jika panjang sisi OA = 4 cm, OC = 7 cm dan OD = 5 cm. Tentukanlah
Jawab
(2). Operasi Penjumlahan dan Pengurangan Pada Vektor
Operasi penjumlahan pada atau pengurangan pada vector secara analitis dilakukan dengan cara menjumlahkan atau mengurang komponen-komponennya, sehingga:
Untuk lebih jelasnya ikutilah contoh soal berikut ini:
05. Jika a = 3 i – j + 2 k , b = –4i + 2 j + 5 k dan c = i + 4 j – 6 k , tentukanlah hasil dari :
(a) 2 a – b + 3 c
(b) a + 2 b – 2 c
Jawab
06. Diketahui titik A(4, –3, –2) dan B(2, 1, –3). Jika AB + BC = –9 + 4 + 6 , maka tentukanlah koordinat titik C
Jawab
Misalkan koordinat C(x, y, z), maka
Jadi
x – 2 = –7 maka x = –5
y – 2 = 0 maka y = 2
z + 3 = 7 maka z = 4